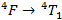Étude de [Co(H2O)6]2+

Manipulations réalisées en travaux pratiques à l'ENS Paris-Saclay

Dans cette partie, nous allons étudier le complexe [Co(H2O)6]2+. Pour cela, il suffit de placer du chlorure de cobalt dans de l'eau distillée. On réalise des spectres d'absorption pour les solutions formées, puis on cherche à en déduire des caractéristiques du complexe.

Partie expérimentale

Produits

Matériel

Mode opératoire

On prépare 4 solutions de [Co(H2O)6]2+ de concentrations respectives 10-2, 5.10-2, 10-1 et 3.10-1 mol.L-1. Pour cela, prélever respectivement :

I - Spectre d'absorption UV-visible et coefficient d'extinction molaire

Les solutions obtenues sont de couleur rose de plus en plus foncée à mesure que la concentration augmente. On enregistre alors les spectres d’absorption de ces quatre solutions entre 300 et 900 nm. On obtient le graphique suivant :

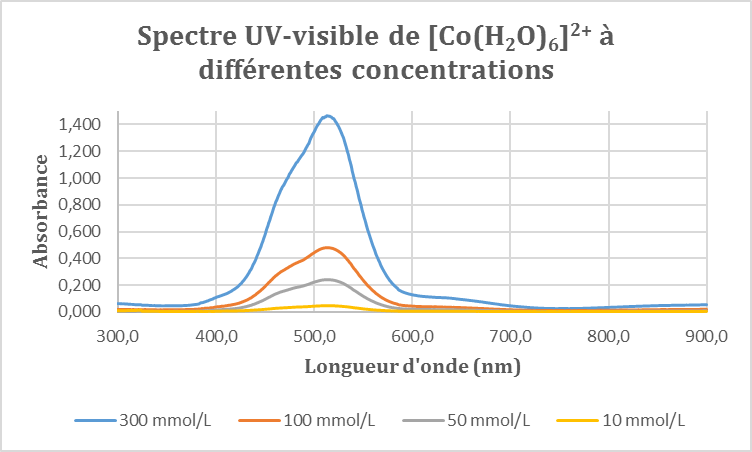
On observe un unique pic d’absorbance autour de 514 nm. On remarque par ailleurs un épaulement de ce pic d‘absorbance à 472 nm.

Dans un premier temps, nous avons voulu déterminer le coefficient d’extinction molaire (ou absorptivité molaire) associé au complexe [Co(H2O)6]2+ à 514 nm car l’intensité de l’autre pic est difficile à lire sur le graphique. Pour cela, on se place à la longueur d’onde du maximum d’absorbance pour les quatre solutions et on relève les absorbances correspondantes. Le maximum est atteint à 514 nm, on relève les absorbances correspondantes puis on trace la courbe correspondante en fonction de la concentration de chacune des solutions. D’après la loi de Beer–Lambert, on sait que :

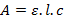
Où :

Ainsi nous devrions obtenir une droite passant par l’origine dont le coefficient directeur nous permettrait de déterminer le coefficient d’extinction molaire ε.

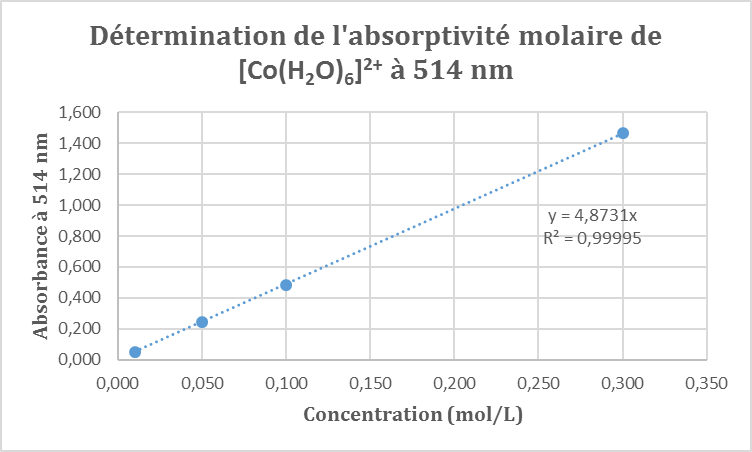
C’est bien le cas : nous obtenons une fonction linéaire avec un très bon coefficient de corrélation. Cela nous permet de déterminer le coefficient d’extinction molaire du complexe :

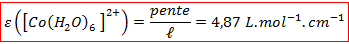
II - Détermination des paramètres du champ cristallin

A partir de ces résultats expérimentaux, nous allons pouvoir déterminer certaines caractéristiques moléculaires de notre complexe. Intéressons–nous à son paramètre de champ cristallin Δ et à son paramètre de Racah B. Pour les déterminer, nous allons nous servir du diagramme de Tanabe–Sugano. Le cobalt se trouve au degré d’oxydation (+II) dans le complexe aqua et possède donc une configuration d7. De plus, le complexe est à champ faible donc nous pouvons remplir les orbitales t2g et eg de la façon suivante :

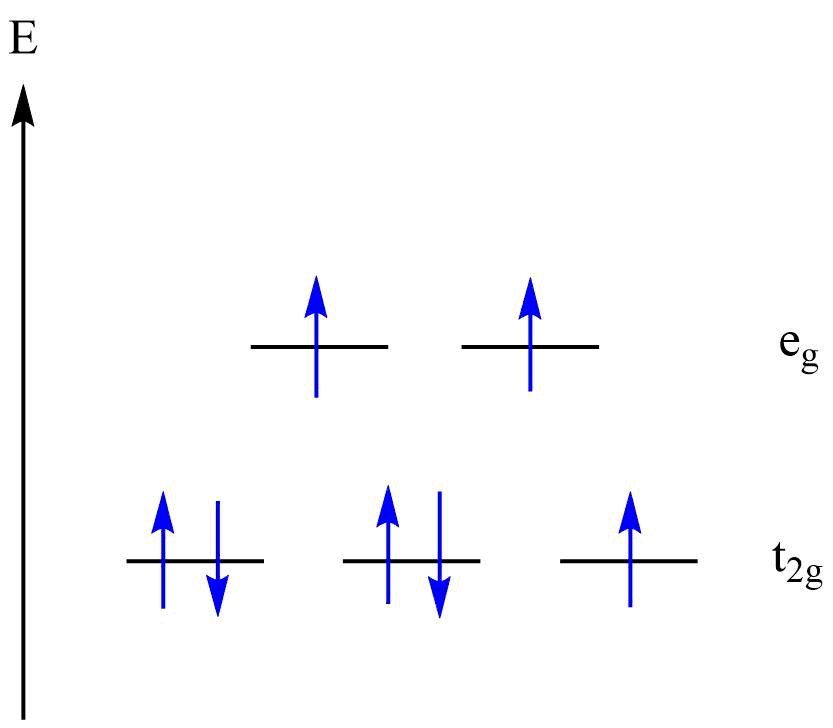
Remplissage des orbitales t2g et eg pour le complexe [Co(H2O)6]2+

Le terme spectroscopique fondamental de l’ion libre en configuration électronique d7 se détermine à partir de la connaissance du moment cinétique orbital L et du moment cinétique de spin S :

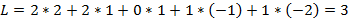
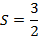
Finalement, le terme spectroscopique fondamental est :

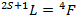
On peut maintenant utiliser le diagramme de Tanabe–Sugano pour un ion d7 en symétrie octaédrique :

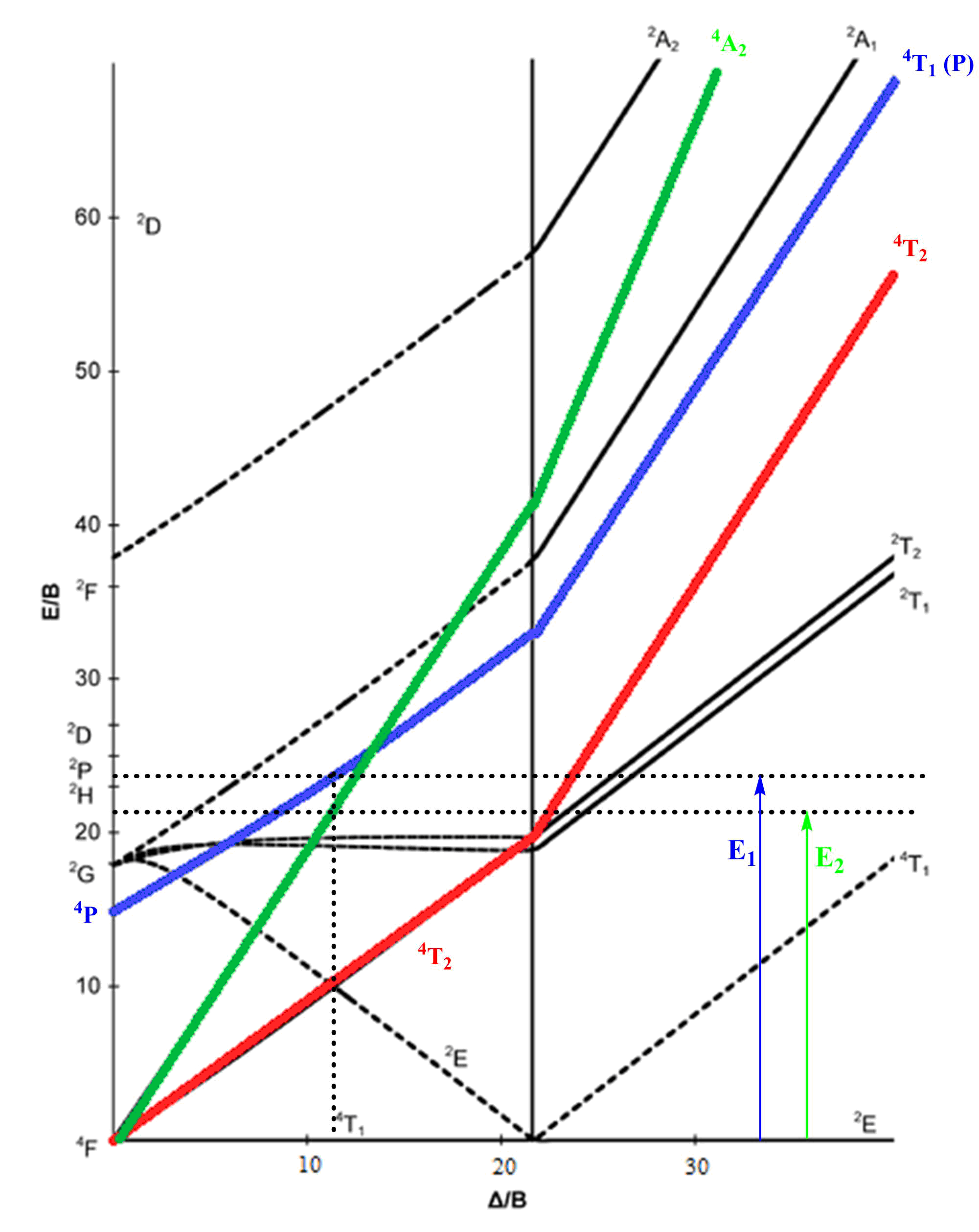
On a repassé en couleur les transitions permises de spin : il en existe trois.

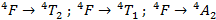
Les longueurs d’onde associées au maximum d’absorption et à l’épaulement vont nous permettre de déterminer le rapport d’énergie de ces deux transitions :

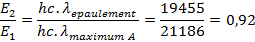
On cherche alors sur le diagramme où ce rapport d’énergie est vérifié entre le terme spectroscopique fondamental et deux autres termes. Il se trouve que ce rapport est vérifié pour la courbe bleue et la courbe verte pour :

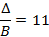
On détermine alors les rapports d’énergie sur le paramètre de Racah correspondants :

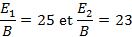
Les deux valeurs obtenues sont très cohérentes. On peut maintenant en déduire le paramètre de champ cristallin :

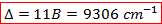
La valeur donnée dans la littérature est de 9300 cm-1. Malgré les erreurs de lecture grossière sur le diagramme de Tanabe – Sugano, on obtient une valeur vraiment très proche de la théorie : notre manipulation nous permet donc l’obtention de résultats très satisfaisants.

Par ailleurs, à l’aide du paramètre de Racah, nous pouvons quantifier le pourcentage d’ionicité de la liaison métal–ligand. Pour cela, on calcule le paramètre β défini par :

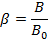
Où B0 est un paramètre théorique connu valant 1120 cm-1. Ainsi on calcule le pourcentage d’ionicité de la liaison :

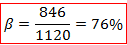
C’est donc une liaison très fortement ionique qui relie les ligands au cobalt. Nous pouvons comparer ce résultat avec le pourcentage d’ionicité obtenu par la relation de Pauling à partir des électronégativités du cobalt et de l’oxygène :

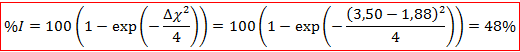
Ces deux résultats sont à peu près cohérents même si les valeurs sont éloignées. La liaison semble bien au moins à moitié ionique.

III - Lien entre le spectre d'absorption et les transitions électroniques

On peut corréler les résultats précédents avec le spectre d’absorption que l’on observe expérimentalement. On s’attendrait à trois pics mais on n’en observe qu’un seul avec un léger épaulement. Selon le diagramme de Tanabe–Sugano, la transition qui devrait se réaliser à la plus faible énergie est la transition :

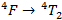
Cependant, cette transition n’est pas observée. Ce n’est pas surprenant dans la mesure où la longueur d’onde associée à cette transition se situe dans le proche infrarouge. On peut le prouver à l’aide du paramètre de Racah B que l’on vient de déterminer :

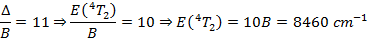
On en déduit la longueur d’onde à laquelle on devrait observer le pic d’absorption :

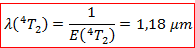
Il est donc normal de ne pas voir cette transition sur notre spectre. Elle aurait dû avoir lieu dans le domaine infrarouge, au-delà de notre domaine de balayage.

On en déduit alors que l’épaulement correspond à la transition :

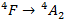
Et que le pic d’absorption correspond à la transition :